The curious case of the random walker

Before I get too hung up on the IFS thing, as pretty as the pictures are, I thought I'd do a simpler one.


Friends, have you ever had one of those nights when you just can't find your way home? Have you ever walked from Leith to Land's End, trying to find a black cab? Have you ever measured distance in pints (or points)? If so, your path might have looked like this:
























Figure 1: A random walker
Surprisingly, the path of an individual who has had one glass too many can make for an interesting picture. So let's so how we can do it.


First of all, it's nowt but points, all the way down. So, all we need to do is show how you plot one point after another, following a path that can vary
rather radically from one moment to the next.

It's useful to know at this pint that one point is one pixel, and pixels are rectangular, in fact, more or less square. So, each pixel has a certain number of neighbours, which it more or less touches. There are two traditional notions of this connectedness, as we call it, and they are sometimes known as 4-c and 8-c. Here is a picture of 4-c.













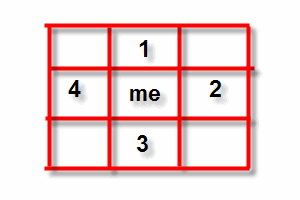
Figure 2: 4-connectedness


So, there you are, a lone point on an endless grid system, and who is around you but your connected pixel neighbours. To your north, number 1, to your east number 2, to your south number 3 and to your west number 4. That's 4-connectedness. And you could go any of those directions.

You should be able to figure out pretty quickly what 8-connectedness means, because there are four unlabelled pixels in that picture. If you prefer, you can consider those other four diagonally connected pixels to be connected as well. That's 8-c. Simple enough. The numbering of the individual pixels isn't important. What matters is that you could go four (or eight) different ways from where you are, if you take a single step.
Now, suppose that we plot where you are, and then plot every other pixel you walk to, on a random walk. Also suppose, for the time being, that you can go to any of those four connected neighbours.

Depending on your sobriety, at every step you take you might change direction, or you might wander in straight lines for a while before lurching off in another direction.

Given that your current position is (x,y), the directions you might go next are illustrated in Figure 3, based on a graphical coordinate system, in which x increases to the right, and y increases as you go down.










Figure 3: Your four neighbours

I think it's time for some processing routines...

First of all, to do this we need to be able to randomly pick a direction to go. We can write that very easily in a little function as follows:

int newDirection4(){ return (int) random(4); }

This returns 0, 1, 2 or 3. That's four numbers. We can say that 0 is north, 1 is east, 2 is south, and 3 is west.

Also, if we start at a point x, we can get a new point x based on those directions as follows:

Point newPoint4(Point oldPoint, int direction)

{
Point temp = oldPoint;

switch(direction)

{ case 0 : //north

{ temp.y = temp.y - 1; break;

}

case 1 : //east
{ temp.x = temp.x + 1; break;

} case 2 : //south
{ temp.y = temp.y + 1; break;


} case 3 : //west

{ temp.x = temp.x - 1; break;

}

}

return temp;

}

[Yes, I know that's a case statement. YOu could do an if too of course. Have we done these yet?]

The thing to notice here is that you return a point that changes either x or y by one pixel, depending on the choice of direction.

Then you plot the next point.

Now repeat! That's almost it. What else could you do? There are quite a few things you can do to liven this up:

• pick a different colour every so often, or for each different random walker
• iterate this for a certain number of iterations, or until some condition occurs, such as bumping into another walker
• change colour every so often
• change how often you change direction, perhaps even depending on how many points you've had.
• do different things when you bump into an existing path (either your own, or another walker's)
• change the size of a "point", for example, increase the stroke width to 2 or more.

One thing you will certainly have to incorporate is rules for what you do when you reach a "wall". By wall, I mean the edge of the area that we have decided to show, such as a 500 x 500 grid. The thing is, there's no point wandering off beyond this grid and plotting where you are, because you will no longer be visible. So, to remain visible, you could, for example, reflect off the wall, or you could "wrap around" and reappear on the other side of the grid. I prefer the "reflecting" or "bouncing" option.

To bounce, you need a rule implemented in a method like this:

Point bounce(Point p)
{
if (p.x > WIDTH)
{ --p.x; }

else if (p.x <> //munged on paste

{ ++p.x; }
else if (p.y > HEIGHT)
{ --p.y; }

else if (p.y <> //mangled code on paste

{ ++p.y; }

return p;

}

If you do this after you compute a new point, you will be able to correct your position so that you do not plot points that are off the grid.

The image in figure 1 is formed from a random walk in which the direction was changed every 2 steps. And, of course, if you pick direction randomly, you will get a different picture every time.

Here is an example of a top-level function that calls the other functions I've mentioned. You could invoke this with an argument of the order of 50,000, to get that many steps.

void iterate(int iterations)

{

//start at middle

Point start = new Point(WIDTH/2,HEIGHT/2);

point(start.x,start.y);

int direction = newDirection4(); //random direction

for(int i = 0; i <> //huh? what happened to my code?

{

if(i % STEPS == 0)

{ direction = newDirection4();

}
start = newPoint4(start,direction); System.out.println(start); point(start.x,start.y);

}
}
Let's see what happens if we increase the step size, so that the direction is only changed every four steps. We can do this in the above routine by setting STEPS = 4.
Figure 4: Purple random walker with STEPS == 4
Let's see what happens if we add another walker in orange, perhaps.
To do this, we might create an array of Points. The first point will represent the first walker, and the next the second walker. We can also change the colour of each walker by using an array of colours. We can use the same index into the two arrays.
At this point we will need to keep track of where each walker is and their colour, so I'll add a routine that can use those two pieces of information:

[what you really want here is a Walker class, but they haven't read the OO stuff yet... pity. This complicates things considerably. A side-effect of this is that you want to make all your variables global... However...]

So this code is pretty nasty, and a first draft, but we'll look at it again later to see what can be done for it...

void iterate()
{
//walkers starting positions randomly

for(int i = 0; i <>

{ walkers[i] = new Point((int) random(WIDTH), (int) random (HEIGHT));

directions[i] = newDirection4(); //each walker has a direction also

stroke(colours[i]); //this walker's colour

point(walkers[i].x,walkers[i].y);

}

//now let each walker go for a walk for a number of iterations - constants declared earlier...

for(int walkerNum = 0; walkerNum <>

{

for(int j = 0; j <>

{

showWalker(walkerNum, j);

}

}

}

void showWalker(int w, int its)

{

//naffly, each walker must have the same step size until I do better

if(its % STEPS == 0)

{

directions[w] = newDirection4(); //random direction

}

walkers[w] = newPoint4(walkers[w], directions[w]); stroke(colours[w]); //this walker's colour

point(walkers[w].x, walkers[w].y); //where has that walker got to now?

}

something like that anyway

And now you can get a picture like this

figure n : a fuchsia and an orange walker...

And here are four walkers...

ffigure the next: Four random walkers, randomly walking

And now, it's time for a point.

This is ridiculous - I keep getting another 20 blank lines to delete... Maybe back to firefox again and a check on a pop up blocker? Because as it is, I can't go like this...